Visualización y Análisis de datos espaciales en salud pública
Introducción
Este taller consiste en 3 partes que buscan exponer al alumno a múltiples técnicas de análisis espacial en el contexto de brotes epidemiológicos. Utilizaremos datos ficticios de la pandemia de COVID-19 en Lima metropolitana para aprender a manejar datos espaciales en ‘R’, visualizar múltiples formatos de datos espaciales y analizar la variación espacial del riesgo de COVID-19 incluyendo la detección de clústers (agrupaciones) de casos.
Resultados del aprendizaje
Al final de este taller, usted será capaz de:
- Cargar y manejar datos espaciales en R
- Visualizar múltiples formatos de datos espaciales y sus atributos (variables) correspondientes
- Generar gráficos dinámicos para la exploración de procesos espaciales
- Calcular la densidad kernel para determinar la variación espacial de casos de una enfermedad.
- Determinar clústers (agrupaciones) de eventos distribuidos espacialmente en formato de puntos o polígonos.
Introducción a epidemiología espacial
Desde hace dos décadas se ha dedicado mucho interés a la modelación de datos espaciales, estos análisis se han hecho en múltiples áreas del conocimiento, incluyendo a la geografía, geología, ciencias ambientales, economía, epidemiología o medicina. En esta sección explicaremos brevemente conceptos generales de análisis espacial aplicados a epidemiología.
Puede expandir cada sección para revisar los detalles.
1. ¿Qué son los datos espaciales?
Son todos los datos que presentan un sistema de referencia de coordenadas (SRC, CRS por sus siglas en inglés ).
2. ¿Qué son los Sistemas de Referencia de Coordenadas?
La Tierra tiene forma de un geoide y las proyecciones cartográficas intentan representar su superficie o una parte de ella en un plano (como el papel o la pantalla del computador).
Los Sistemas de Referencia de Coordenadas (SRC ó CRS) nos ayuda a establecer una relación entre cualquier punto de la superficie terrestre con un plano de referencia mediante las proyecciones cartográficas. En general, los SRC se pueden dividir en:
Geográficas.
Proyectados (también denominados Cartesianos o rectangulares)

3. Proyecciones geográficas
El uso de SRC geográficos es muy común y el más empleado. Están representadas por la latitud y longitud y tienen como unidad de medida a los grados sexagesimales. El sistema más popular se denomina WGS 84.
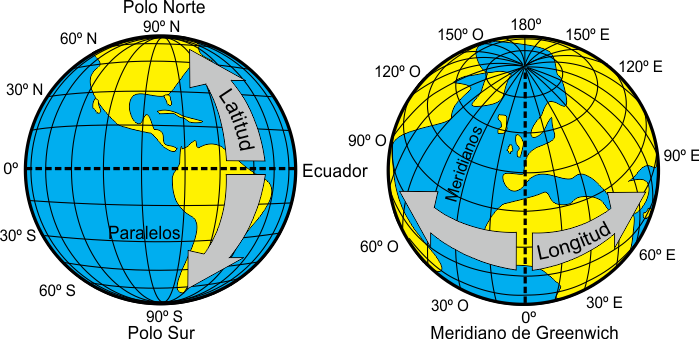
Créditos: A. Barja, 2021
4. Proyecciones cartográficas
Entre todas las proyecciones que existen, ninguna es la mejor en un sentido absoluto, depende de las necesidades específicas a la hora de usar el mapa.
La mayoría de las proyecciones que se emplean hoy en día en la cartografía son proyecciones modificadas, híbridos entre varios tipos de proyecciones que minimizan las deformaciones y permiten alcanzar resultados predeterminados.
Según sus propiedades prevalecientes, las proyecciones se distinguen entre equidistantes, equivalentes y conformes; dependiendo de si mantienen la fidelidad representando distancias, áreas o ángulos respectivamente.
Según el tipo de superficie sobre el que se realiza la proyección, existen tres proyecciones básicas:
Las proyecciones cilíndricas; son efectivas para representar las áreas entre los trópicos.
La proyecciones cónicas; sirven para representar áreas en latitudes medias.
Las proyecciones azimutales; sirven para representar zonas en altas latitudes.

Créditos: mapnetico, 2020
Proyección cartográfica más empleada
- Universal Tranverse Mercator (UTM)
Proyección cilíndrica conforme que gira el cilindro en 90 ° y divide el elipsoide de referencia en segmentos de 6 grados de ancho (60 segmentos para llegar a los 360°). UTM está diseñado para minimizar las distorsiones dentro de la misma área. cerca del meridiano central, la distorsión es mínima y aumenta alejándose del meridiano. Es recomendable utilizar UTM sólo con mapas muy detallados.
5. Códigos EPSG
Todos los Sistemas de Referencia de Coordenadas (SRC ó CRS) llevan asociados un código que los identifica de forma única y que a través del cual podemos conocer los parámetros asociados al mismo. Se conoce como Spatial Reference System Identifier (SRID) inicialmente impulsado por el European Petroleum Survey Group (EPSG).
Los códigos EPSG más conocidos son: - WGS84: 4326 - UTM zona 17N: 32617 - UTM zona 18N: 32618 - UTM zona 18S: 32718
6. Introducción a la estadística espacial
Las técnica de estadística clásica suponen estudiar variables aleatorias que se consideran independientes e idénticamente distribuidas (i.i.d.). Por ello, al momento de analizar fenómenos que varían en tiempo y espacio se requiere una modelación que considere la (auto)correlación espacial o temporal.
Cuando se tienen datos espaciales intuitivamente se tiene la noción de que las observaciones cercanas están correlacionadas, por ello es necesario utilizar herramientas de análisis que consideren dicha estructura.
7. ¿Por qué es especial lo espacial?
Primera Ley de Waldo Tobler
“Todo está relacionado con todo lo demás, pero las cosas más cercanas están más relacionadas que las distantes”. (Tobler,1970)
Autocorrelación espacial
Es la correlación entre los valores de una sola variable estrictamente atribuible a sus posiciones de ubicación cercanas en una superficie bidimensional. Esto introduce una desviación del supuesto de iid.
Para medir la autocorrelación espacial existen test estadísticos, entre ellos:
Test de Mantel
Test de Moran
Test C Geray
Para mayor detalle recomendamos la introducción del libro Geocomputation with R de Robin Lovelace, Jakub Nowosad, Jannes Muenchow.
Paquetes requeridos
Los siguientes paquetes (disponibles en CRAN o gitHub) son necesarios para el análisis.
# install.packages("remotes")
# install.packages("tidyverse")
# install.packages("sf")
# install.packages("mapview")
# install.packages("GADMTools")
# remotes::install_github("paleolimbot/ggspatial")
# install.packages("leaflet")
# install.packages("leaflet.extras2")
# install.packages("spdep")
# install.packages("spatstat")
# install.packages("raster")
# install.packages("smacpod")
# install.packages("ggspatial")Cuando los paquetes estén instalados se necesita abrir una nueva sesión de R. Luego, cargar las siguientes librerías:
library(tidyverse)
library(sf)
library(mapview)
library(GADMTools)
library(ggspatial)
library(leaflet)
library(leaflet.extras2)
library(spdep)
library(spatstat)
library(raster)
library(smacpod)
library(ggspatial)Caso de estudio
Para este taller utilizaremos una base de datos ficticia que fue creada
usando como referencia los datos abiertos del Gobierno
Peruano.
Esta base contiene los registros de cada persona diagnosticada de
COVID-19 por el Ministerio de Salud (MINSA) hasta el 24-MAY-2020.
Los datos de georefenciación (coodenadas) de los casos fueron simulados para los propósitos de este taller. Puede descargar directamente la base de datos del repositorio de Zenodo
covid <- read_csv(url("https://zenodo.org/record/4915889/files/covid19data.csv?download=1"))| FECHA\_CORTE | UUID | DEPARTAMENTO | PROVINCIA | DISTRITO | METODODX | EDAD | SEXO | FECHA\_RESULTADO | rango\_edad | lon | lat |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2021-05-22 | c66bf87eadf9c1a4bb60cc06674bc0ff | LIMA | LIMA | ANCON | PR | 66 | MASCULINO | 2020-04-03 | 60-79 | -77.10665 | -11.78599 |
| 2021-05-22 | bee5549e6caae07009d3845471721dc9 | LIMA | LIMA | ANCON | PR | 47 | FEMENINO | 2020-05-28 | 40-59 | -77.06849 | -11.70551 |
| 2021-05-22 | b40562fc3db1160bab9d0f0ef46d57ef | LIMA | LIMA | ANCON | PR | 29 | MASCULINO | 2020-09-11 | 20-39 | -77.07175 | -11.75761 |
| 2021-05-22 | 494a959a21abea9d197dccdc553150d4 | LIMA | LIMA | ANCON | PR | 36 | MASCULINO | 2020-09-11 | 20-39 | -77.08505 | -11.67503 |
| 2021-05-22 | 8f0d79f9de7a2e949ff755f62ceec80b | LIMA | LIMA | ANCON | PR | 33 | MASCULINO | 2020-09-11 | 20-39 | -77.06757 | -11.67211 |
| 2021-05-22 | 78c435fe9d3401a0f3ac305b9d3c04ed | LIMA | LIMA | ANCON | PR | 39 | FEMENINO | 2020-09-30 | 20-39 | -77.17340 | -11.67811 |
| 2021-05-22 | 397e6e6091f8c92086969e49ada5a6c4 | LIMA | LIMA | ANCON | PR | 44 | FEMENINO | 2020-09-30 | 40-59 | -77.11325 | -11.75787 |
| 2021-05-22 | e323742fdffd02a1e7ec0dba2a1a8c5d | LIMA | LIMA | ANCON | PR | 45 | FEMENINO | 2020-09-30 | 40-59 | -77.04202 | -11.63406 |
| 2021-05-22 | eed80d87469c769c32483350b2e1e569 | LIMA | LIMA | ANCON | PR | 49 | FEMENINO | 2020-09-30 | 40-59 | -77.13583 | -11.81147 |
| 2021-05-22 | 82fc799ec2aa425d0e5405adb62ad31f | LIMA | LIMA | ANCON | PR | 49 | FEMENINO | 2020-09-30 | 40-59 | -77.11790 | -11.80319 |
| 2021-05-22 | 70b6e956e6f2812f037979fca2abc019 | LIMA | LIMA | ANCON | PR | 49 | FEMENINO | 2020-09-30 | 40-59 | -77.13552 | -11.77465 |
| 2021-05-22 | 7cb47912dafe1aa8018888bfe9109197 | LIMA | LIMA | ANCON | PR | 45 | FEMENINO | 2020-10-01 | 40-59 | -77.05448 | -11.60338 |
| 2021-05-22 | ef13e230a1bbd58e893250846d340dd8 | LIMA | LIMA | ANCON | PR | 30 | FEMENINO | 2020-09-16 | 20-39 | -77.19165 | -11.78114 |
| 2021-05-22 | bdb2677329adb2c4f604aeda50fc8e8f | LIMA | LIMA | ANCON | PR | 32 | FEMENINO | 2020-09-30 | 20-39 | -77.11297 | -11.81771 |
| 2021-05-22 | 755186c6529502fd4615a6a0c49e16cf | LIMA | LIMA | ANCON | PR | 37 | FEMENINO | 2020-09-16 | 20-39 | -77.09455 | -11.65914 |
| 2021-05-22 | e949cab78173cdfc5a6e0c5c5e71b5b2 | LIMA | LIMA | ANCON | PR | 44 | FEMENINO | 2020-09-16 | 40-59 | -77.02234 | -11.63633 |
| 2021-05-22 | 007de2f79d821c5a6875bb1465c2f2f7 | LIMA | LIMA | ANCON | PR | 40 | FEMENINO | 2020-09-16 | 40-59 | -77.15927 | -11.76954 |
| 2021-05-22 | f90fb726b97e3fd5bdc956ae66f2751f | LIMA | LIMA | ANCON | PR | 44 | FEMENINO | 2020-09-16 | 40-59 | -77.18581 | -11.69466 |
| 2021-05-22 | a0d2f7cf23e2a989a5d18e4f857156b4 | LIMA | LIMA | ANCON | PR | 33 | FEMENINO | 2020-09-24 | 20-39 | -77.15870 | -11.72663 |
| 2021-05-22 | b160905c9fa1c1bcfcdd917ada970016 | LIMA | LIMA | ANCON | PR | 35 | FEMENINO | 2020-09-16 | 20-39 | -77.08235 | -11.76282 |
Manejo de datos espaciales
R tiene un gran universo de paquetes para representación y análisis
espacial. Actualmente existen 2 formatos predominantes:
sp
y sf. Para los fines de este taller
utilizaremos sf ya que tiene una integración natural con el ecosistema
tidyverse.
Existen múltiples variedades de representaciones gráficas con datos espaciales. En este curso nos enfocaremos en la representación espacial de 1) patrones de puntos y 2) datos de polígonos ( e.j. por áreas administrativas ).
Patrones de puntos
Si tenemos una base de datos georeferenciada (con coordenadas geográficas para cada observación) podemos utilizar estos valores ( coordenadas ) para transformar nuestra base de datos tabular en una base de datos espacial.
Usaremos la función
st_as_sf()para especificar los valores de latitud y longitud. Adicionalmente, tenemos que especificar el sistema de referencia de coordenadas (CRS en ingles) con que fueron georeferenciados nuestros datos en el área de estudio ( ej. crs = 4326 ).
covid_p <- covid %>%
st_as_sf(coords = c("lon", "lat"), crs = 4326)Haremos un gráfico simple usando ggplot2 y la geometría geom_sf().
covid_p %>%
filter(FECHA_RESULTADO == "2020-12-11") %>%
ggplot() +
geom_sf() 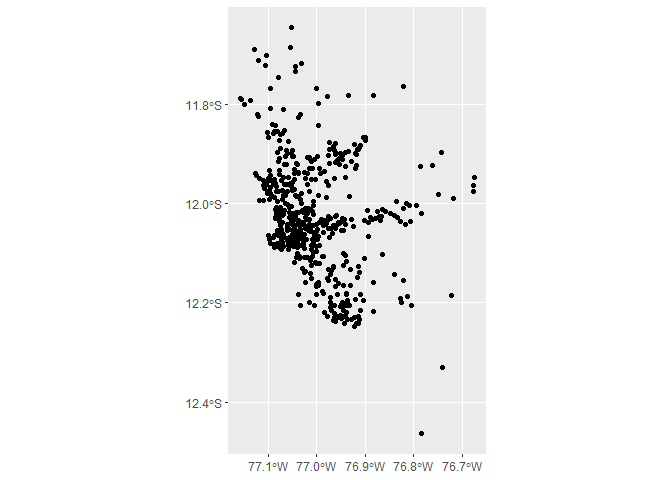
Para visualizar nuestro mapa de una forma dinámica podemos usar el
paquete mapview().
m_p <- covid_p %>%
filter(FECHA_RESULTADO == "2020-12-10") %>%
mapview(layer.name = "puntos")
m_p
Datos en polígonos
Para realizar las representaciones de las áreas necesitamos un archivo
que contiene la geometría espacial (los bordes), hay varios formatos
pero el más conocido es el shapefile (.shp).
Uno puede cargar los datos del archivo
.shpusando la funciónst_read(). Para este taller utilizaremos el paqueteGADMToolsque contiene los datos espaciales de las divisiones políticas de todos los países.GADMToolsdescarga datos en formatogadm_sfdel cual extraeremos el objeto sf con la funciónpluck().
peru <- gadm_sf_loadCountries("PER", level=3)
lima_sf <- peru %>%
pluck("sf") %>%
# Filtramos los datos espaciales solo de Lima metropolitana
filter(NAME_2 == "Lima") %>%
# Editamos algunos errores en nuestros datos espaciales
mutate(NAME_3 = ifelse(NAME_3 == "Magdalena Vieja",
"Pueblo Libre", NAME_3))Ahora procesaremos los datos de la base covid y los datos espaciales
lim_sf para poder hacer la unión.
Como nuestra base de datos es a nivel individual, haremos el conteo del número de observaciones para cada fecha y distrito. Construiremos unos datos de tipo
panel, para lo cual completaremos con0todas las fechas de las unidades geográficas que no reportaron casos.
covid_count <- covid %>%
group_by(DISTRITO, FECHA_RESULTADO) %>%
summarise(casos = n()) %>%
ungroup() %>%
complete(FECHA_RESULTADO = seq.Date(min(FECHA_RESULTADO, na.rm =T),
max(FECHA_RESULTADO, na.rm = T),
by="day"),
nesting(DISTRITO), fill = list(n = 0))
covid_sf <- lima_sf %>%
mutate(DISTRITO = toupper(NAME_3)) %>%
full_join(covid_count, by = "DISTRITO", "FECHA_RESULTADO")
class(covid_sf)## [1] "sf" "data.frame"
Haremos un gráfico simple para verificar que nuestros datos estén proyectados en el lugar correcto.
covid_sf %>%
filter(FECHA_RESULTADO == "2020-12-11") %>%
ggplot() +
geom_sf()
m_sf <- covid_sf %>%
filter(FECHA_RESULTADO == "2020-12-11") %>%
mapview(layer.name = "distritos")
m_sf
Múltiples capas
Los contenidos en los mapas suelen representarse como capas, las cuales, podemos combinarlas y sobreponerlas para entender el evento de interés.
Cada capa es agregada como una geometría diferente con
geom_sf(). En mapview podemos usar el símbolo+para graficar ambas capas.
ggplot() +
geom_sf(data = covid_sf %>%
filter(FECHA_RESULTADO == "2020-12-11")) +
geom_sf(data = covid_p %>%
filter(FECHA_RESULTADO == "2020-12-11"))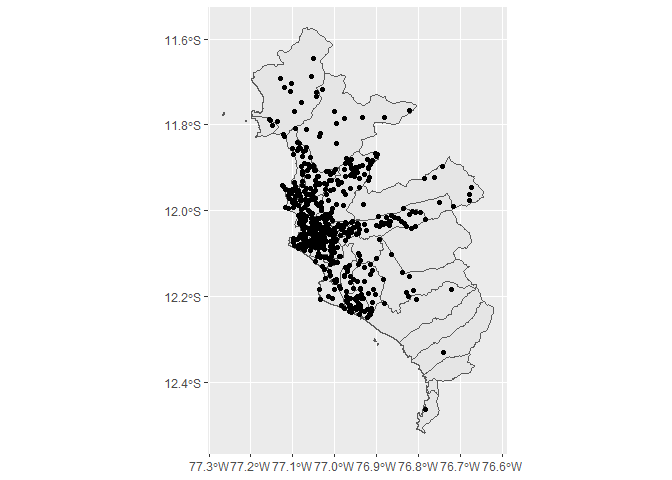
m_p + m_sf
Visualización de datos espaciales
Ahora exploraremos algunas variables de interés en la base de datos para comprender mejor la transmisión de la enfermedad.
Patrones de puntos
Al utilizar la base de datos a nivel individual podemos cambiar las características de nuestra geometría (puntos) de acuerdo a los atributos que deseamos graficar.
Una variable
Usaremos el color de la geometría (argumento
col) para representar el sexo de los pacientes con COVID-19 la base de datos.
covid_p %>%
filter(FECHA_RESULTADO == "2020-12-11") %>%
ggplot() +
geom_sf(aes(col = SEXO), alpha = .2) +
facet_wrap(.~SEXO)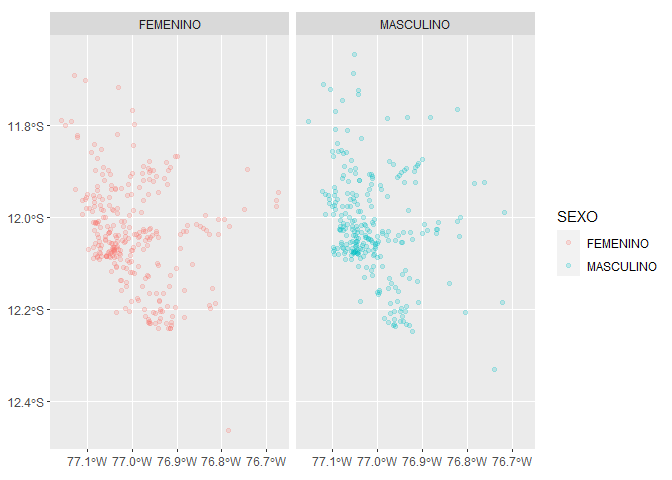
En el caso de la visualización dinámica con mapview el color se asigna
con el argumento zcol. Usaremos el argumento burst = T para que cada
categoría (de la variable asignada en zcol) se visualice como una capa
separa y pueda seleccionarse u ocultarse en el mapa.
covid_p %>%
filter(FECHA_RESULTADO == "2020-12-11") %>%
mapview(layer.name = "points", zcol = "SEXO", burst = T)
Dos o mas variable
Al igual que con los gráficos de datos tabulares, podemos explorar las visualizaciones con facetas y dividir los datos de acuerdo a sub-grupos focalizados.
covid_p %>%
filter(FECHA_RESULTADO == "2020-04-11" |
FECHA_RESULTADO == "2020-12-11") %>%
ggplot() +
geom_sf(aes(col = SEXO), alpha = .2) +
facet_grid(SEXO~FECHA_RESULTADO) +
guides(col = F)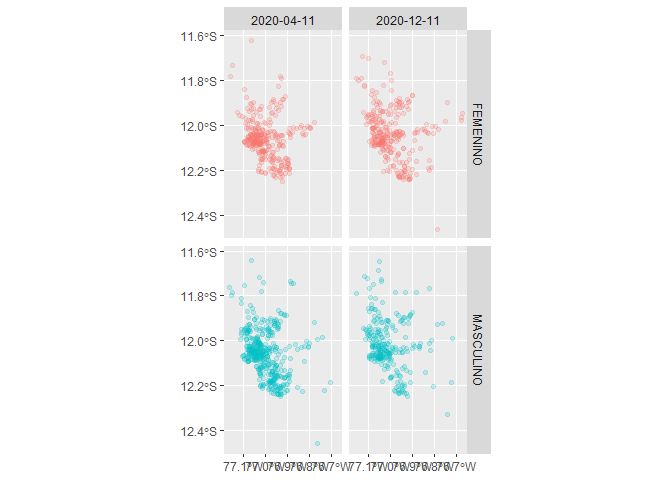
mapview permite agrupar múltiples capas con los operadores + y |.
Más detalles en la documentación del
paquete.
m1 <- covid_p %>%
filter(FECHA_RESULTADO == "2020-04-11") %>%
mapview(zcol = "SEXO", layer.name = "2020-04-11 - SEXO")
m2 <- covid_p %>%
filter(FECHA_RESULTADO == "2020-12-11") %>%
mapview(zcol = "SEXO", layer.name = "2020-12-11 - SEXO")m1 + m2
Composición
Podemos usar las mismas herramientas usadas para la creación gráficos de
datos tabulares para generar una mejor composición de nuestra
representación espacial. Podemos modificar las escalas de color (
scale_color_*() ) y el tema ( theme_*() ) entro otros. Cuando
representamos datos espaciales es importante representar la escala
espacial de los datos y el norte. Ambas características pueden
ser graficadas con el paquete ggspatial.
covid_p %>%
filter(FECHA_RESULTADO == "2020-12-11") %>%
ggplot() +
geom_sf(data = covid_sf) +
geom_sf(aes(col = EDAD), alpha = .2) +
scale_color_viridis_c(option = "B") +
annotation_scale() +
annotation_north_arrow(location = "tr",
style = north_arrow_nautical)+
theme_bw()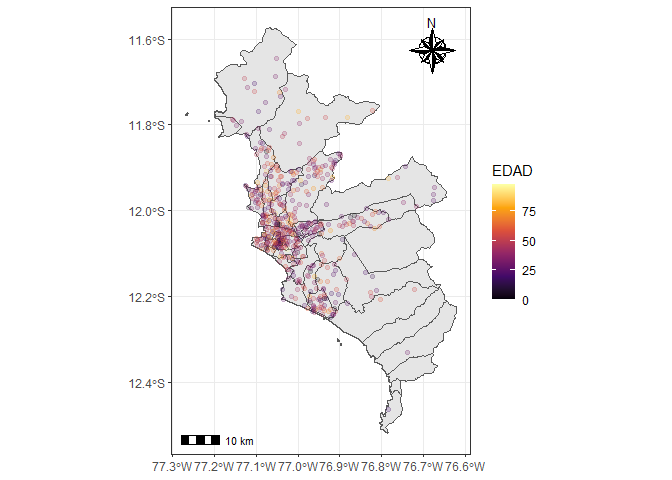
Datos en polígonos
La forma de reporte más común de los sistemas de vigilancia de enfermedades infecciosas es la agrupación de casos por unidades geográficas o administrativas. En esta sección exploraremos la representación de datos en polígonos espaciales.
Una variable
Usaremos el relleno de la geometría (argumento
fill) para representar el número de casos de COVID-19 por distritos en Lima metropolitana. Importante notar que el argumento color (col) se usa para definir el color de los bordes de la geometría.
covid_sf %>%
filter(FECHA_RESULTADO == "2020-12-11") %>%
ggplot() +
geom_sf(aes(fill = casos))
En el caso de la visualización dinámica con mapview el relleno también
se asigna con el argumento zcol.
covid_sf %>%
filter(FECHA_RESULTADO == "2020-12-11") %>%
mapview(layer.name = "casos", zcol = "casos")
Dos o mas variable
Seleccionaremos 2 fechas para comparar la evolución de la epidemia.
covid_sf %>%
filter(FECHA_RESULTADO == "2020-04-11" |
FECHA_RESULTADO == "2020-12-11") %>%
ggplot() +
geom_sf(aes(fill = casos)) +
facet_grid(.~FECHA_RESULTADO)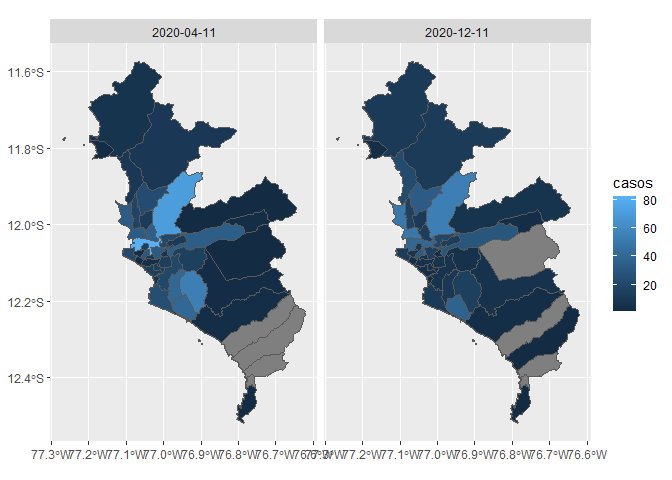
También podemos visualizar la distribución espacial de ambas fechas de forma dinámica.
d1 <- covid_sf %>%
filter(FECHA_RESULTADO == "2020-04-11") %>%
mapview(zcol = "casos", layer.name = "2020-04-11 - casos")
d2 <- covid_sf %>%
filter(FECHA_RESULTADO == "2020-12-11") %>%
mapview(zcol = "casos", layer.name = "2020-12-11 - casos")d1 + d2
Composición
Al igual que con los datos de puntos, podemos usar las mismas herramientas para generar una mejor composición de nuestra representación espacial.
covid_sf %>%
filter(FECHA_RESULTADO == "2020-12-11") %>%
ggplot() +
geom_sf(aes(fill = casos)) +
scale_fill_viridis_c(option = "F", direction = -1) +
annotation_scale() +
annotation_north_arrow(location = "tr",
style = north_arrow_nautical)+
theme_void()
Otro paquete importante de revisar para la representación de estructuras espaciales es:
tmap.
Variación espacial del riesgo
En esta sección se brindará una introducción a una metodologías para obtener representaciones gráficas de procesos espaciales como el riesgo de una enfermedad. En este taller exploraremos la estimación de la densidad kernel para datos espaciales que representan procesos discretos (ej. brotes). Existen otras técnicas para datos espaciales que representan procesos continuos (ej. precipitación) como Kriging.
Para estimar la densidad del kernel definiremos una ventana espacial
de análisis usando la función owin del paquete
spatstat
covid_subset <- covid %>%
filter(FECHA_RESULTADO == "2020-05-05")
covid_win <- owin(xrange = range(covid_subset$lon),
yrange = range(covid_subset$lat))Luego, definiremos el objeto patrón de puntos ( ppp ) a partir de los registros de casos.
covid_ppp <- ppp(covid_subset$lon,
covid_subset$lat,
window = covid_win)Finalmente, el objeto de la clase densidad lo convertiremos a uno de
clase rasterLayer. Eliminaremos las áreas fuera de nuestra zona de
estudio usando la función mask y utilizando nuestro objeto espacial de
los limites de Lima metropolitana (lima_sf).
densidad_raster_cov <- raster(density(covid_ppp, bw.ppl),
crs = 4326) %>%
mask(lima_sf)La densidad puede ser representada de la siguiente forma:
densidad_raster_cov %>%
mapview()
Detección de clústers
En esta sección se brindará una introducción a algunos métodos para detectar la agrupación espacial de casos o clústers en diferentes tipos de datos espaciales.
Datos de patrones puntuales:
Estadísticas de escaneo espacial (Spatial Scan Statistics-SSS):
Para realizar el cálculo de las estadísticas de escaneo espacial, primero es necesario emplear datos de la clase patrones de puntos o ppp :
En este ejemplo, para definir una variable binaria, usaremos los casos detectados por PCR como infecciones recientes (positivo) y por otros métodos (ej. Prueba de Anticuerpos - PR) como infecciones pasadas (negativos).
covid_subset_posi <- covid %>%
filter(FECHA_RESULTADO == "2020-05-05") %>%
mutate(positividad = ifelse(METODODX == "PCR", 1, 0))
covid_scan_ppp <- ppp(covid_subset_posi$lon,
covid_subset_posi$lat,
range(covid_subset_posi$lon),
range(covid_subset_posi$lat),
marks = as.factor(covid_subset_posi$positividad))Aplicaremos la prueba de escaneo espacial propuesto por M.
Kulldorff en SatScan e implementada en
R en el paquete smacpod.
Por motivos de costo computacional utilizaremos 49 simulaciones (
nsim) de Monte Carlo para determinar el valor-p de la prueba de hipótesis. Para otros propósitos se recomienda incrementar el número de simulaciones.
covid_scan_test <- spscan.test(covid_scan_ppp,
nsim = 49, case = 2,
maxd=.15, alpha = 0.05)El objeto de tipo spscan contiene información del clúster detectado:
locids: las localizaciones incluidas en el clústercoords: las coordenadas del centroide del clústerr: el radio del clústerrr: el riesgo relativo (RR) dentro del clústerpvalue: valor=p de la prueba de hipótesis calculado por simulaciones de Monte Carlo
entre otros.
covid_scan_test## $clusters
## $clusters[[1]]
## $clusters[[1]]$locids
## [1] 1103 1371 1092 1375 1381 1104 1380 1378 1091 1074 1097 1376 1089 1076 1373
## [16] 1379 1096 1087 1088 1095 2093 2122 2117 2102 2106 1105 2121 1107 605 2086
## [31] 1098 592 1101 2111 596 2096 1070 599 2120 597 971 2094 2119 607
##
## $clusters[[1]]$coords
## [,1] [,2]
## [1,] -77.0472 -12.11374
##
## $clusters[[1]]$r
## [1] 0.02709301
##
## $clusters[[1]]$pop
## [1] 44
##
## $clusters[[1]]$cases
## 110344
## 31
##
## $clusters[[1]]$expected
## [1] 11.17098
##
## $clusters[[1]]$smr
## 110344
## 2.775046
##
## $clusters[[1]]$rr
## 110344
## 2.873837
##
## $clusters[[1]]$propcases
## 110344
## 0.7045455
##
## $clusters[[1]]$loglikrat
## [1] 20.05829
##
## $clusters[[1]]$pvalue
## [1] 0.02
##
##
##
## $ppp
## Marked planar point pattern: 2316 points
## Multitype, with levels = 0, 1
## window: rectangle = [-77.18195, -76.64829] x [-12.468713, -11.634232] units
##
## attr(,"class")
## [1] "spscan"
Para representar gráficamente el clúster detectado, el subconjunto de análisis es convertido a una clase adecuada para la representación espacial.
# Construimos el centroide del clúster
cent <- tibble(lon = covid_scan_test$clusters[[1]]$coords[,1],
lat = covid_scan_test$clusters[[1]]$coords[,2]) %>%
st_as_sf(coords = c("lon", "lat"), crs = 4326, remove = F)
# Construimos el área del clúster en base al radio
clust <- cent %>%
st_buffer(dist = covid_scan_test$clusters[[1]]$r)Graficaremos el clúster detectado empleando el paquete mapview:
cluster <- mapview(clust, alpha.regions = 0, color = "red")
points <- covid_subset_posi %>%
st_as_sf(coords = c("lon", "lat"), crs = 4326) %>%
mapview(zcol = "positividad", alpha.regions = .4, alpha = 0)
cluster + points
Datos agregados (en polígonos)
Autocorrelación espacial (global): Moran I
Para llevar a cabo el cálculo de estadístico de Moran I global, en primer lugar establecemos el conjunto de datos de análisis. Debido a la estructura longitudinal de la base de datos, filtraremos por una fecha en específico.
covid_sf_subset <- covid_sf %>%
filter(FECHA_RESULTADO == "2020-05-05") %>%
mutate(casos = replace_na(casos, 0))Luego, a partir de la distribución de los polígonos (distritos) en el área de estudio definiremos la matriz de vecindad.
covid.nb <- poly2nb(covid_sf_subset, queen=TRUE,snap = 0.13)Con la matriz de vecindad llevamos a cabo el cálculo de la matriz de pesos espaciales
covid.lw <- nb2listw(covid.nb, style="W", zero.policy=TRUE)Finalmente, realizamos el cálculo de la prueba de Moran global I:
moran.test(covid_sf_subset$casos, covid.lw)##
## Moran I test under randomisation
##
## data: covid_sf_subset$casos
## weights: covid.lw
##
## Moran I statistic standard deviate = 3.0548, p-value = 0.001126
## alternative hypothesis: greater
## sample estimates:
## Moran I statistic Expectation Variance
## 0.090491242 -0.023809524 0.001399995
nota: La prueba implementada por defecto utiliza un cálculo analítico del estadístico de Moran I. Esta prueba, sin embargo, es muy susceptible a polígonos distribuidos irregularmente. Por ello actualmente el paquete
spdepcuenta con una versión de la prueba que se basa en simulaciones de Monte Carlo, la cual puede ser llevada a cabo con la funciónmoran.mc.
Autocorrelación espacial (local): Getis Ord
Para el cálculo de la autocorrelación espacial local, en primer lugar establecemos los umbrales (del estadístico z) a partir de las cuales se definen lo clúster de valores altos y bajos.
breaks <- c(-Inf, -1.96, 1.96, Inf)
labels <- c("Cold spot",
"Not significant",
"Hot spot")Realizamos el cálculo del estadístico de Getis Ord
covid_lg <- localG(covid_sf_subset$casos, covid.lw)
covid_sf_lisa<-covid_sf_subset %>%
mutate(cluster_lg=cut(covid_lg, include.lowest = TRUE,
breaks = breaks,
labels = labels))Finalmente realizamos el gráfico:
covid_sf_lisa %>%
ggplot() +
geom_sf(aes(fill=cluster_lg)) +
scale_fill_brewer(name="Clúster",
palette = "RdBu", direction=-1) +
theme_bw()
Se puede visualizar que en la zona central y sur de lima la existencia de clústers espaciales de alta y baja concentración de casos respectivamente.
Sobre este documento
Contribuciones
- Gabriel Carrasco-Escobar, Antony Barja & Jesus Quispe: Versión inicial
Contribuciones son bienvenidas vía pull requests.
